Unidad V. Aplicaciones de la derivada
5.3 Prueba de la primera derivada para la determinación de máximos y mínimos.
5.3 Prueba de la primera derivada para la determinación de máximos y mínimos.
Se llama Criterio de la primera derivada al método o teorema
utilizado frecuentemente en el cálculo matemático
para determinar los mínimos y máximos relativos
que pueden existir en una función
mediante el uso de la primera derivada
o derivada principal, donde se observa el cambio de signo, en un intervalo abierto señalado que contiene al punto crítico
 .
.
Teorema valor máximo y mínimo
"Sea  un punto crítico de una función
un punto crítico de una función  que es continua en un intervalo abierto
que es continua en un intervalo abierto  que contiene a
que contiene a  . Si
. Si  es derivable en el intervalo, excepto posiblemente en
es derivable en el intervalo, excepto posiblemente en  , entonces
, entonces  puede clasificarse como sigue."
puede clasificarse como sigue."
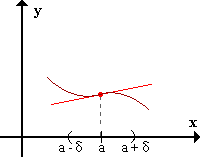
1. Si

'

cambia de positiva a negativa en

, entonces

tiene un máximo relativo en

.
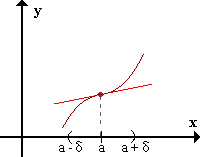
2. Si

'

cambia de negativa a positiva en

, entonces

tiene un mínimo relativo en

.
3. Si

'

es positiva en ambos lados de

o negativa en ambos lados de c, entonces

no es ni un mínimo ni un máximo relativo.
Definición: Si un número c está en el dominio de una función f, c se conoce como un número crítico (valor crítico) de f si f’(c) = 0 ó f’(c) no existe.
A continuación una guía para construir la gráfica de una función usando la derivada:
1) Halla f’(x) (la derivada de f).
2) Halla los números críticos, igualando f’(x) a cero y resolviendo para x. Incluir también todos los valores de x donde la derivada no existe (es decir, no está definida).
3) Evalua cada número crítico c en la función f para obtener los puntos críticos.
4) Localiza los puntos hallados en el paso anterior (3) en el plano cartesiano.
5) Determina en qué intervalo la función es creciente, decreciente o constante, usando el signo de la derivada. (Es decir, usa el teorema).
6) Dibuja la gráfica, de manera que sea creciente en el intervalo donde la derivada es positiva, decreciente en el intervalo donde la derivada es negativa y horizontal en el intervalo donde la derivada es igual a cero.
Tema: Valores Extremos (Máximos y Mínimos Absolutos)
Si f es una función continua en el intervalo [a,b], entonces existe un número c en el intervalo [a,b] tal que f(c)>f(x) para todo x en el intervalo [a,b]. En este caso, f(c) se conoce como un valor máximo (o máximo absoluto) de f.
Si f(c) es el máximo de f en el intervalo [a,b] se dice que f alcanza su máximo en c, y en ese caso, el punto (c,f(c)) es el punto más alto de la gráfica.
Análogamente, si existe un número c en el intervalo [a,b] tal que f(c)<f(x) para todo x en el intervalo [a,b], entonces f(c) es un valor mínimo (o mínimo absoluto) de f.
Si f(c) es el mínimo de f en el intervalo [a,b] se dice que f alcanza su mínimo en c, y en ese caso, el punto (c,f(c)) es el punto más bajo de la gráfica.
A los valores máximos y mínimos de una función en un intervalo cerrado se les conoce como valores extremos o extremos de la función en el intervalo.

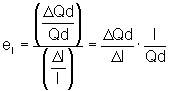

 .
. un punto crítico de una función
un punto crítico de una función  que es continua en un intervalo abierto
que es continua en un intervalo abierto  que contiene a
que contiene a  . Si
. Si  es derivable en el intervalo, excepto posiblemente en
es derivable en el intervalo, excepto posiblemente en  , entonces
, entonces  puede clasificarse como sigue."
puede clasificarse como sigue." '
' cambia de positiva a negativa en
cambia de positiva a negativa en  , entonces
, entonces  tiene un máximo relativo en
tiene un máximo relativo en  .
. '
' cambia de negativa a positiva en
cambia de negativa a positiva en  , entonces
, entonces  tiene un mínimo relativo en
tiene un mínimo relativo en  .
. '
' es positiva en ambos lados de
es positiva en ambos lados de  o negativa en ambos lados de c, entonces
o negativa en ambos lados de c, entonces  no es ni un mínimo ni un máximo relativo.
no es ni un mínimo ni un máximo relativo.