1.2 Dominio y rango de una función.

Unidad I. Funciones.
1.2 Dominio y rango de una función.

Dominio:
El dominio de una función está dado por el conjunto de valores que puede tomar una función.
 Por ejemplo si f(x) = x;  esta variable x puede tomar cualquier valor, no tiene ninguna restricción, entonces su dominio esta compuesto por todos los números Reales.

En general se pueden seguir las siguientes recomendaciones para obtener el dominio de una función o de una expresión algebraica:

• No puede haber una raíz cuadrada ( ó cualquier raíz par ) negativa, pues se trataría de un número imaginario que no hace parte de los Reales.
• Un fraccionario no puede contener por denominador cero, pues la expresión queda indeterminada.

Rango:

El rango de una función, está determinado por todos los valores que pueden resultar al evaluar una función. Son los valores obtenidos para la variable dependiente (y). También se puede expresar como todos los valores de salida de la función.

Por ejemplo:

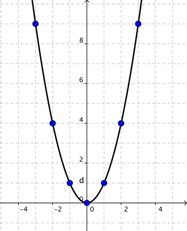
 f(x) = x^2

Si x=2, evaluamos f(2) = 2 ^2 = 4. Y así podemos hacerlo con cualquier número, positivo o negativo. Como x está elevada al cuadrado todos los valores resultantes (es decir de salida) son positivos. Con lo anterior se obtiene que el rango está conformado por el cero y todos los números positivos.

Al graficar la función se obtiene:

.