5.4 Concavidad, puntos de inflexión y prueba de la segunda derivada.

Unidad V. Aplicaciones de la derivada.
5.4 Concavidad, puntos de inflexión y prueba de la segunda derivada.

5.4 Concavidad, puntos de inflexión y prueba de la segunda derivada. 

Concavidad y puntos de inflexión

La segunda derivada de una función también proporciona información sobre el comportamiento de ésta. Para iniciar este estudio daremos la siguiente:

	Definición  de concavidad
	Se dice que la gráfica de una función f es cóncava hacia arriba en un intervalo A, , si  es creciente sobre A. Si  es decreciente sobre A entonces se dice que la gráfica de f es cóncava hacia abajo.

Note que es la función derivada  la que debe ser creciente o decreciente en el intervalo A.

En la siguiente representación gráfica, una función f es cóncava hacia arriba en el intervalo  y cóncava hacia abajo en el intervalo 

	Teorema 5
	Si f es una función tal que  cuando , entonces la gráfica de fes cóncava hacia arriba sobre . Demostración: Si  y como , entonces se tiene que  es creciente sobre  por lo que de acuerdo con la definición de concavidad de una función, se obtiene que f es cóncava hacia arriba sobre .

 

	Teorema 6
	Si f es una función tal que  cuando , entonces la gráfica de fes cóncava hacia abajo sobre . Demostración: De la hipótesis: , y como , se obtiene que  es decreciente sobre  por lo que según la definición dada sobre concavidad, la gráfica de la función f es cóncava hacia abajo sobre .

Punto de inflexión

f presenta un punto de inflexión en x=a si existe δ > 0 / para todo x perteneciente a (a - δ,a) f(x) > f'(a)(x-a) + f(a) y para todo x perteneciente a (a,a + δ) f(x) < f'(a)(x-a) + f(a) (o viceversa: f menor a la izquierda y mayor a la derecha).

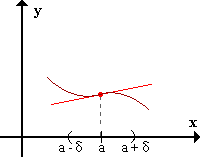		En el semientorno izquierdo de a, f está por encima de la tangente a f(x) en a, y en el semientorno derecho de a, f está por debajo de la tangente.
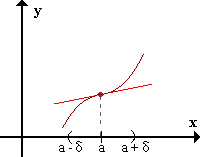Actividad Interactiva		En el semientorno izquierdo de a, f está por debajo de la tangente a f(x) en a, y en el semientorno derecho de a, f está por encima de la tangente.